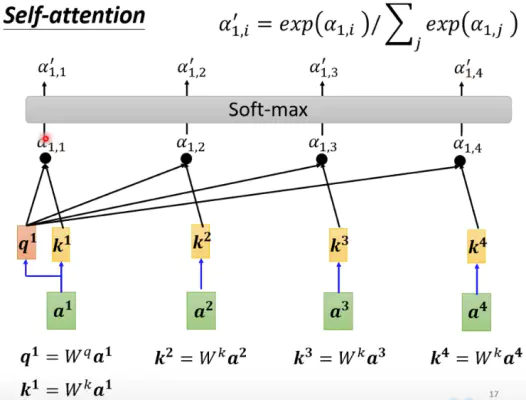
attention
词向量: $x_1$(早),$x_3$(上),$x_3$(好)
$x_ix_i^T$ : 表征两个向量的夹角,表征一个向量在另一个向量上的投影,投影的值大,说明两个向量相关度高
归一化 -> 权重
$z_1$(早) = $[0.476,0.428,0.096]$
即: 分配0.476权重给予本身 , 0.428的权重给予”上” , 0.096的权重给予”上”
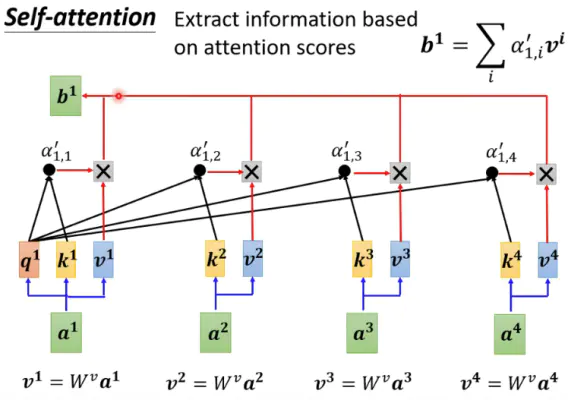
加权求和 -> attention向量
$n$ : 输入词向量个数
$d$ : dimension of input,输入向量维度,d = dimension of X = 4
$d_k$ : dimension of k ,即K的行维度,可取 = $d$ = dimension of $x$
$d_v$ : dimension of v ,即V的行维度,可取 = $d$ = dimension of $x$
($W^q,W^k,W^v$ 变换矩阵,可学习参数)
self-attention pytorch Implement
import torch
from torch import nn
import numpy as np
class SelfAttention(nn.Module):
def __init__(self,input_dim,key_dim=None,value_dim=None):
super(SelfAttention, self).__init__()
self.input_dim = input_dim
if key_dim is None:
self.key_dim = input_dim
if value_dim is None:
self.value_dim = input_dim
self.query = nn.Linear(self.input_dim,key_dim,bias=False)
self.key = nn.Linear(self.input_dim, key_dim, bias=False)
self.value = nn.Linear(self.input_dim, value_dim, bias=False)
self.norm_fact = 1 / np.sqrt(key_dim)
# X->[batch_size ,seq_len,input_dim]
def forward(self,X):
query = self.query(X)
key = self.key(X)
value = self.value(X)
keyT = key.permute(0, 2, 1) # key[batch_size ,seq_len,input_dim] -> [batch_size,input_dim,seq_len]
attention = nn.Softmax(dim=-1)(torch.bmm(query,keyT)) * self.norm_fact
output = torch.bmm(attention,value)
return output
model = SelfAttention(4,5,3)
X = torch.rand(1,3,4)
print(X)
output = model(X)
print(output)
print(output.size())
tensor([[[0.9641, 0.7163, 0.9725, 0.6660],
[0.2968, 0.2546, 0.8528, 0.9114],
[0.0058, 0.5362, 0.1145, 0.9804]]])
tensor([[[-0.0294, 0.1206, 0.1320],
[-0.0314, 0.1191, 0.1306],
[-0.0329, 0.1189, 0.1299]]], grad_fn=<BmmBackward0>)
torch.Size([1, 3, 3])
Multi-head Self-Attention


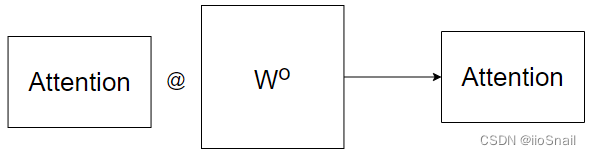
$heads=2,dim=4$,拆分向量维度值head_dim = dim / heads = 2
shift $XW:[seqlen,dim]->[heads,seqlen,\frac{dim}{heads}]$
multi-head attetion pytorch Implement
import torch
from torch import nn
import numpy as np
'''
Self-Attention Shape [batch_size,seq_len,intput_dim]
Multi-Head Attention Shape [batch_size,heads,seq_len,(intput_dim/heads)]
'''
def attention(query, key, value):
key_dim = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) / np.sqrt(key_dim)
attention_weight = scores.softmax(dim=-1)
return torch.matmul(attention_weight, value)
class MultiHeadAttention(nn.Module):
def __init__(self, heads, input_dim):
super(MultiHeadAttention, self).__init__()
assert input_dim % heads == 0 # 可整除
self.key_dim = input_dim // heads
self.heads = heads
self.linears = [
nn.Linear(input_dim, input_dim),# W-Q
nn.Linear(input_dim, input_dim),# W-K
nn.Linear(input_dim, input_dim),# W-V
nn.Linear(input_dim, input_dim),# W-O
]
def forward(self, x):
batch_size = x.size(0)
query, key, value = [
linear(x).view(batch_size, -1, self.heads, self.key_dim).transpose(1, 2)
for linear, x in zip(self.linears, (x, x, x))
]
#x shape:[batch_size,heads,seq_len,input_dim/heads]
x = attention(query, key, value)
#x shape:[batch_size,seq_len,input_dim]
x = (x.transpose(1, 2).contiguous().view(batch_size, -1, self.heads * self.key_dim))
return self.linears[-1](x)
mutil_head_model = MultiHeadAttention(2,4)
output = mutil_head_model(X)
print(output)
print(output.size())
tensor([[[ 0.1228, -0.1211, 0.5368, -0.1685],
[ 0.1230, -0.1210, 0.5374, -0.1690],
[ 0.1229, -0.1207, 0.5375, -0.1683]]], grad_fn=<AddBackward0>)
torch.Size([1, 3, 4])
transformer
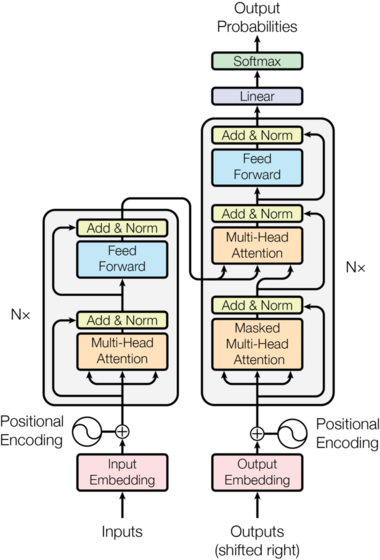
PositionalEncoding
[!NOTE]
self-attention的无序性丢失了词语的位置信息,Positional Encoding对句中词语的相对位置进行编码,保证词语的有序性
$[0,1,…,T]$作为位置编码,如第3个词的编码:[3,3,3,3,…,3],当句子过长时最后一个词的值比首词相差较大,合并embedding后易造成特征倾斜,若归一化,即$[0/T,1/T,…,T/T]$作为位置编码可避免特征倾斜问题,但导致不同文本的位置编码步长不一致,如:
[!NOTE] Note
利用sin,cos的特性使得位置编码分布处于[0,1]区间,同时位置编码的步长一致,由于其周期性会导致不同pos而位置编码一致的情况,因此 pos/X 可试周期无限长并交替使用sin和cos,从而避免
$pos$ : 单词所在句中位置
$2i$ : 偶数维度
$2i+1$ : 奇数维度
$dim$ : 编码维度
$X=[0.1,0.2,0.3,0.4],pos=2,posCode=[sin(\frac{2}{10000^{\frac{0}{4}}}),cos(\frac{2}{10000^{\frac{0}{4}}}),sin(\frac{2}{10000^{\frac{2}{4}}}),cos(\frac{2}{10000^{\frac{2}{4}}})]$
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout: float = 0.1, max_len: int = 64):
super().__init__()
self.dropout = nn.Dropout(p=dropout)
position = torch.arange(max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))
pe = torch.zeros(max_len, 1, d_model)
pe[:, 0, 0::2] = torch.sin(position * div_term)
pe[:, 0, 1::2] = torch.cos(position * div_term)
self.register_buffer('pe', pe)
def forward(self, x: Tensor) -> Tensor:
#x: Tensor, shape [seq_len, batch_size, embedding_dim]
x = x + self.pe[:x.size(0)]
return self.dropout(x)
encoder
decoder
$Y:shifted-right-output$
note : 我有一只猫 -> I have a cat
$Y$:[begin] -> I,[begin,I]->have,[begin,I,have]->a,[begin,I have a ]->cat
class FeedForward(nn.Module):
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(self.w_1(x).relu()))
maskedMultiHeadAttention
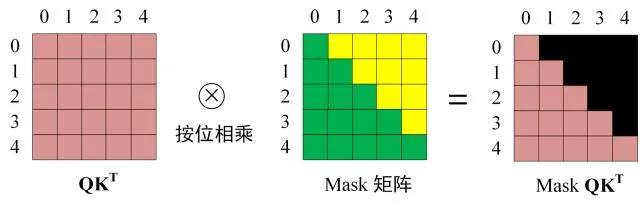
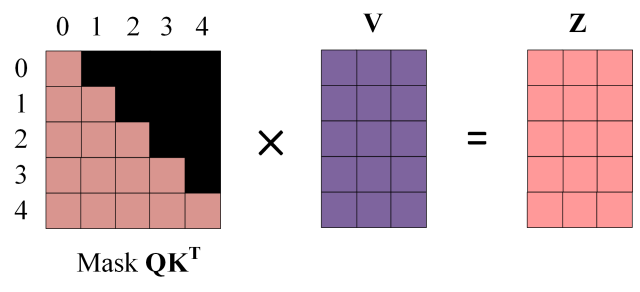

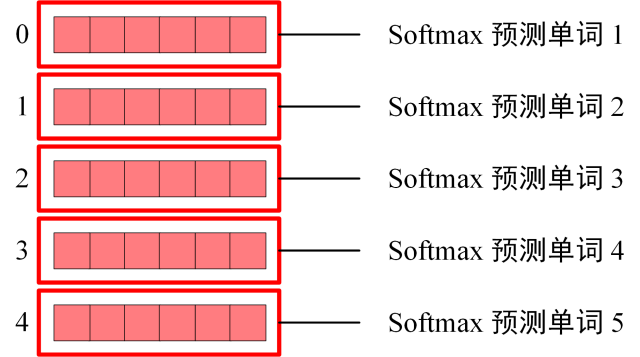
[!NOTE] Note
train时经masked后传入整个输入矩阵等同于推理时按词顺序挨个推理
def generate_square_subsequent_mask(size: int) -> Tensor:
#size:
return torch.triu(torch.full((size, size), float('-inf')), diagonal=1)
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
transformer implement
#waiting
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!