数据结构(2) 线性表 ~ 今天的风儿甚是喧嚣 JiaoPan

线性表的定义

线性表是具有相同数据类型的$n$个数据元素的有限序列
除第一个元素,每个元素有且仅有一个直接前驱,除最后一个元素,每个元素有且仅有一个后继

顺序表

线性表的顺序存储称为顺序表,用一组地址连续的存储单元依次存储线性表中的数据元素，因此逻辑上相邻的两个元素在物理位置上也相邻

顺序表描述

#define MaxSize 50
typedef struct {
    ElemType data[MaxSize];//顺序表元素 静态分配
    int length;//当前长度
}SqList;

#define InitSize 100
typedef struct {
    ElemType *data;//顺序表元素 动态分配数组的指针
    int MaxSize,length;//数组最大容量和当前元素个数
}SqList;

L.data = (ElemType *)malloc(sizeof(ElemType) * InitSize);//c
L.data = new ElemType(InitSize);//C++

顺序表最主要的特点是随机访问,通过首地址和元素序号可在O(1)的时间复杂度内找到指定的元素

插入操作
在顺序表L的第i个位置插入新元素e

bool ListInsert(SqList &L, int i, ElemType e) {
    if (i < 1 || i > L.length+1)
        return false;
    if (L.length > = MaxSize)
        return false;
    for (int index = L.length; index >= i; index--)
        L.data[index] = L.data[index - 1];
    L.data[i-1] = e;
    L.length++;
    return true;
}

删除操作
删除顺序表L中第i个位置的元素,删除的元素用引用变量e返回

bool ListDelete(SqList &L, int i, ElemType &e) {
    if (i < 1 || i > L.length)
        return false;
    e = L.data[i - 1];
    for (int index = i; index < L.length; index++)
        L.data[index-1] = L.data[index];
    L.length--;
    return true;
}

按值查找
在顺序表L中查找一个元素值等于e的元素,并返回其位置(非索引)

int ListDelete(SqList L,ElemType e) {
    int index;
    for (index = 0; index < L.length; index++)
        if (L.data[index] == e)
            return index + 1;
    return 0;
}

1.长度为$n$的顺序表$L$,编写一个时间复杂度为 $O(n)$ 、空间复杂度为 $O(1)$ 的算法，该算法删除线性表中所以值为x的数据元素。

void delX(Sqlist &L,ElemType x){
    int k = 0 ;
    for(int i = 0;i < L.length;i++){
        if(L[i] != x){
            L.data[k] = L.data[i];
            k++;
        }
    }
    L.length = k;
}

2.从有序顺序表中删除所有其值重复的元素，使表中所有的值均不相同。

bool delSame(Sqlist &L){
    if(L.length = 0)
        return false;
    int i,j;
    for(i = 0,j = 1;j < L.length;j++){
        if(L.data[i] != L.data[j])
            L.data[++i] = L.data[j];
    }
    L.length = i;
    return true;
}

3.将两个有序顺序表合并成一个新的有序顺序表，并由函数返回其结果顺序表。

bool merge(Sqlist A,Sqlist B,Sqlist &C){
    if(A.length + B.length > C.maxSize)
        return false;
    int i = 0,j = 0,k = 0;
    while(i < A.length && j < B.length){
        if(A.data[i] <= B.data[j])
            C.data[k++] = A.data[i++];
        else
            C.data[k++] = B.data[j++]
    }
    while(i < A.length){
        C.data[k++] = A.data[i++];
    }
    while(j > B.length){
        C.data[k++] = B.data[j++];
    }
    C.length = k+1;
    return true;
}

4.线性表 $(a_1,a_2,...,a_n)$ 中的元素递增有序存储于计算机内，设计算法完成在最短的时间内在表中查找数值为x的元素，若存在则将其与后继元素交换，否则插入表中并使表中元素仍然递增有序。

void searchExchangeInsert(Sqlist &L,ElemType x){
    int low = 0,high = n -1,mid;
    while(low <= high){
        mid = (low + high) / 2;
        if(L.data[mid] == x)
            break;
        else if(L.data[mid] < x)
            low = mid + 1;
        else
            high = mid - 1;
    }
    if(L.data[mid] == x && mid != (n-1)){
        ElemType temp = L.data[mid];
        L.data[mid] = L.data[mid+1];
        L.[mid+1] = temp;
    }
    if(low > high){
        for(int i = n- 1;i > high;i--)
            L.data[i+1] = L.data[i];
        L.data[i+1] = x;
    }
}

5.设将 $n(n>1)$ 个整数存放到一维数组R中。设计一个高效的算法将R中保存的序列循环左移 $p(0<p<n)$ 个位置，即将R中的数据由 $(x_0,x_1,...,x_{n-1})$ 变换为 $(x_p,x_{p+1},...,x_{n-1},x_0,x_1,...,x_{p-1})$

算法思想:

令 $A=(x_0,x_1,...,x_{p-1}),B=(x_p,x_{p+1},...,x_{n-1}),C=BA$ , $A^{-1}=(x_{p-1},x_{p-2},...,x_1,x_0)$

$AB \rightarrow A^{-1}B\rightarrow A^{-1}B^{-1}\rightarrow (A^{-1}B^{-1})^{-1}\rightarrow BA$

void Reverse(int R[],int from,int to){
    for(int i = 0; i < (to-from+1)/2;i++){
        int temp = R[from+i];
        R[from+i] = R[to-i];
        R[to-i] = temp;
    }
}
void Converse(int R[],int n,int p){
    Reverse(R,0,p-1);
    Reverse(R,p,n-1);
    Reverse(R,0,n-1);
}

6.长度为L的升序序列S，处在第[L/2]个位置的输称为S的中位数，两个序列的中位数是含它们所有元素升序序列的中位数，现有两个等长的升序序列A和B，设计算法找出序列A和序列B的中位数。

算法思想：

设 $a$ 为A的中位数， $b$ 为B的中位数

若 $a=b$ ，则 $a$ 或 $b$ 即为所求中位数；
若 $a<b$ ，舍弃序列A中较小的一半，同时舍弃序列B中较大的一半，两次舍弃的长度相等；
若 $a>b$ ，舍弃序列A中较大的一半，同时舍弃序列B中较小的一半，两次舍弃的长度相等；
在保留的两个升序序列中,重复1，2，3,直到两个序列只含有一个元素为止，较小者为所求中位数；

int mediSearch(int A[],int B[],int n){
    int sa=0,da=n-1,ma;
    int sb=0,db=n-1,mb;
    while(sa != da || sb != db){
        ma = (sa+da)/2;
        mb = (sb+db)/2;
        if(A[ma] == B[mb]){
            return A[ma];
        }
        if(A[ma] < B[mb]){
            if((sa+da)%2 == 0){//元素个数为奇数
                sa = ma;
                db = mb;
            }
            else{
                sa = ma + 1;
                db = mb;
            }
        }
        else{
            if((sb+db)%2 == 0){//元素个数为奇数
                da = ma;
                sb = mb;
            }
            else{
                da = ma;
                sb = mb + 1;
            }
        }
    }
    return A[sa] < B[sb]?A[sa]:B[sb];
}

7.已知一个整数序列 $A=(a_0,a_1,...a_{n-1})$ ，其中 $0\leqslant a_{i}\leqslant n$ ,若存在 $a_{p1}=a_{p2}=...a_{pm}=x$ ,且 $m>n/2$ ,则称 $x$ 为A的主元素。例如 $A=(0,5,5,3,5,7,5,5)$ ，5为A的主元素， $B=(0,5,5,3,5,1,5,7)$ ,则B中没有主元素。设计算法找出A的主元素并输出，否则输出-1；

int majority(int A[],int n){
    int i,c,count = 1;//c保存候选主元素
    c = A[0];
    for(i = 1;i < n;i++){
        if(A[i] == c)
            count++;
        else{
            if(count > 0)
                count--;
            else{
                c = A[i];
                count = 1 ;
            }
        }
    }
    if(count > 0)
        for(i = count = 0;i < n; i++){//统计候选主元素实际出现的次数
            if(A[i] == c)
                count++;
        }
    if(count > (n/2))
        return c；
    else
        return -1;
}

链表

由于顺序表的插入、删除操作需要移动大量元素,影响运行效率,由此引入线性表的链式存储,链式存储不需要使用地址连续的存储单元,即逻辑上相邻的元素不要求在物理位置上也相邻

单链表

通过一组任意的存储单元来存储线性表中的数据元素,每个链表节点除了存放元素本身,还需要存放指向后继的指针,其是非随机存取结构

typedef struct Node{
    ElemType data; //XX
    struct Node *next;//指针域
}Node,*LinkList;

通常用头指针来标识一个单链表,在单链表第一个节点前附加一个节点称为头节点,头节点的数据域不设任何信息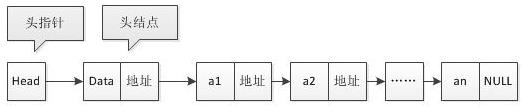

头指针和头节点：
1.不管带不带头节点,头指针始终指向链表的第一个节点
2.引入头节点,统一操作,统一空表和非空表的处理

采用头插法建立单链表

LinkList createList(LinkList &L){
    Node *node;
    int x;
    L = (LinkList)malloc(sizeof(Node));
    L->next = null;
    scanf("%d",&x);
    while(x != 10){
        node = (Node*)malloc(sizeof(Node));
        node->data = x;
        node->next = L->next;
        L->next = node;
        scanf("%d",x);
    }
    return L;
}

采用尾插法建立单链表

LinkList createList(LinkList &L){
    int x;
    L = (LinkList)malloc(sizeof(Node));
    Node *node,*tail = L;
    scanf("%d",&x);
    while(x != 10){
        node = (Node*)malloc(sizeof(Node));
        node->data = x;
        tail->next = node;
        tail = node;
        scanf("%d",x);
    }
    tail->next = null;
    return L;
}

按序号查找节点值

Node* getElem(LinkList L，int i){
    int j=1;
    Node *p= L->next;//头节点
    if(i == 0)
        return L;
    if(i < 1)
        return null;
    while(p && j < i){ //从第一个节点开始查找
        p = p->next;
        j++
    }
    return p;
}

按值查找表节点

Node* getElem(LinkList L，ElemType  e){
    Node *p= L->next;//头节点
    while(p && p->data != e){ //从第一个节点开始查找
        p = p->next;
    }
    return p;
}

插入节点操作

p = getElem(L,i-1);//查找插入位置i的前驱节点
s->next = p->next;
p->next = s;

删除节点操作

p = getElem(L,i-1);//查找删除位置i的前驱节点
q = p-next;
p->next = q->next;
free(q);

双链表

双链表通过prior和next，分别指向前驱节点和后继节点
双链表的按值查找和按位查找操作和单链表相同

typedef struct Node{
    ElemType data;
    struct Node *prior;
    struct Node *next;
}Node,*DoubleList;

插入节点操作

p = getElem(L,i-1);//查找插入位置i的前驱节点
s->next = p->next;
p->next-prior = s;
s->prior = p;
p->next = s;

删除节点操作

p = getElem(L,i-1);//查找删除位置i的前驱节点
q = p-next;
p->next = q->next;
p->next->prior = p;
free(q);

静态链表

静态链表是由数组来描述线性表的链式存储结构,节点也有数据域data和指针域next

#define MaxSize 50
typedef struct{
    ElemType data;
    int next ;//下一个元素的数组下标
}StaticLinkList[MaxSize];

在带头结点的单链表L中，删除所有值为x的结点，并释放其空间。

void deleteX(LinkList &L){
    Node *p = L->next,*pre = L;*q;//pre为p的前驱结点
    while(p != null){
        if(p->data == x){
            q = p;
            p = p->next;
            pre->next = p;
            free(q);
        }
        else{
            pre = p;
            p = p->next;
        }
    }
}

设L为带头结点的单链表，编写算法实现从尾到头反向输出每个结点的值。

//递归方法
void reversePrint(LinkList &L){
    if(L->next != nulll){
        reversePrint(L-next);
    }
    printf(L->data)
}
//借助栈

编写在带头结点的单链表L中删除最小值结点的高效算法，假设最小值唯一。

LinkList deleteMinNode(LinkList &L){
    Node *p = L->next,*pre = L;// pre为p的前驱结点
    Node *minPre = pre,*min = p;//最小值的前驱和当前最小值
    while(p!= null){
        if(p->data < min->data){
            min = p;
            minPre = pre;
        }
        pre = p;
        p = p->next;
    }
    minPre->next = min->next;
    free(min);
    return L;
}

试编写算法将带头结点的链表逆置，且空间复杂度为$O(1)$

LinkList reverse(LinkList L){
    Node *p,*r;//p为工作指针，r为后继指针
    p = L->next;
    L->next = NULL;
    while(p != NULL){
        r = p->next;
        p->next = L->next;
        L->next = p;
        p = r;
    }
}

数据结构数据结构

本博客所有文章除特别声明外，均采用 CC BY-SA 3.0协议。转载请注明出处！