空间域,即包含图像像素的平面,空间域技术直接在图像像素上操作,空间域处理可由下式表示:
g(x,y) = T[f(x,y)]
其中f(x,y)为输入图像,g(x,y)为处理后的图像,T是在点(x,y)的邻域上定义的关于f的一种算子

灰度变换

s = T(r)
s和r分别表示g和f在任意点(x,y)处的灰度

灰度变换函数

• 图像反转 (图像灰度级范围[0,L-1])
  s = L - 1 -r
  该式反转一幅图像的灰度级,可得到等效的照片底片,适用于增强嵌入在图像暗区域中的白色或灰色细节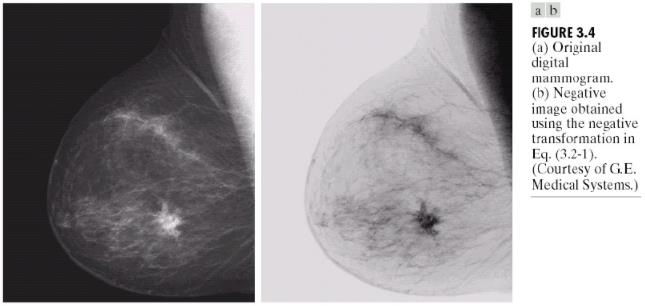
  
• 对数变换
  s = clog(1+r) (c为常数)
  该式将范围较窄的低灰度值映射为范围较宽的灰度值，适用于增强图像中的暗像素值
  
• 幂律(伽马)变换
  s = cr^γ (c和γ为正常数)
  γ < 1 提高灰度级，在正比函数上方，使图像变亮
  γ > 1 降低灰度级，在正比函数下方，使图像变暗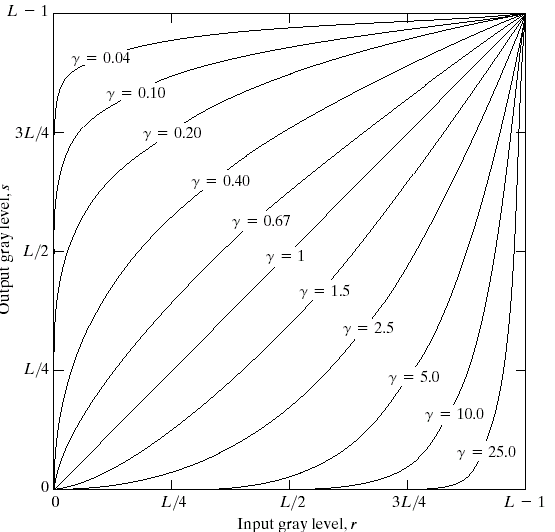
  
  γ = 0.6,0.4,0.3 | c = 1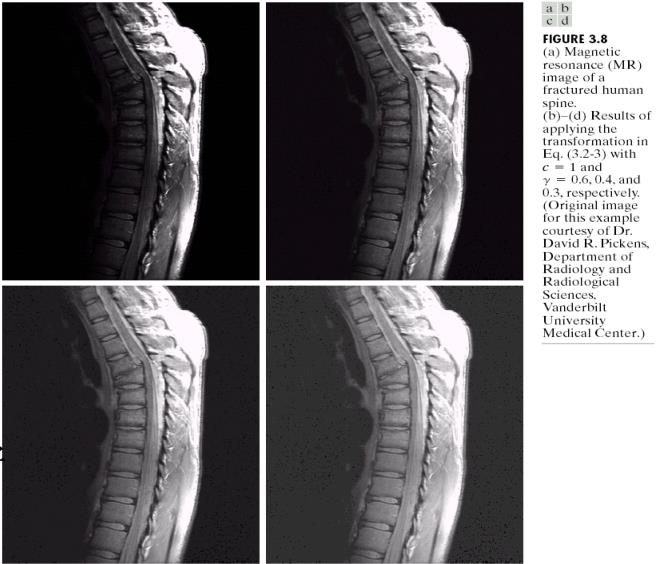
  
  γ = 3,4,5 | c = 1
  

分段线性变换函数

• 对比度拉伸 扩展低对比度图像灰度级动态范围
  点(s1,r1)和点(s2,r2)的位置控制变换函数的形状
  若r1=s1,r2=s2,则变换为线性函数,将产生无变化的灰度级
  若r1=r2,s1=0,s2=L-1,则变换为阈值处理函数,将产生一幅二值图像
  (s1,r1)和点(s2,r2)的中间值产生不同程度的灰度级扩展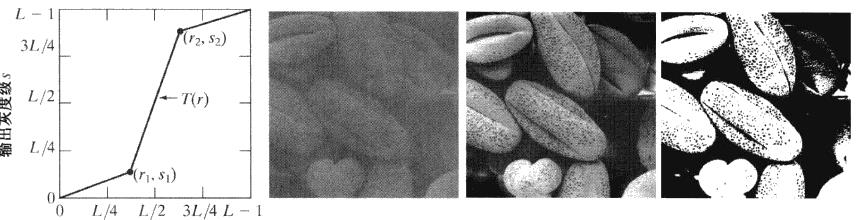
  

• 灰度级分层 突出图像中指定灰度范围的亮度
  将感兴趣范围内的所有灰度值显示为一个值(如白色),而其他值显示为另一个值(如黑色)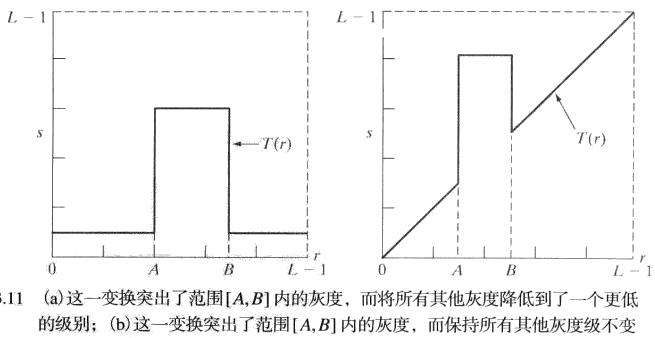
  
  

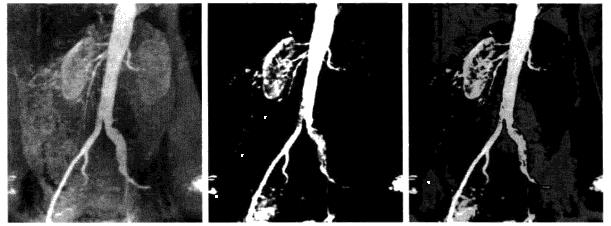
• 比特平面分层
  像素由比特组成的数字,在256级灰度图像中,每个像素由8比特组成,通过突出特定比特来增强图像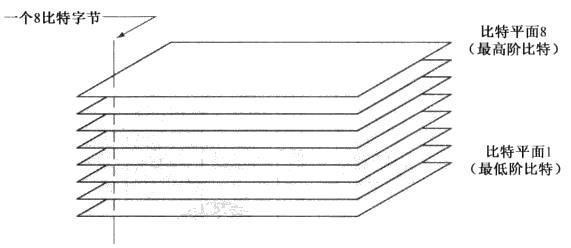
  
  
  存储4个高阶比特平面允许以接受的细节重建图像
  

直方图处理

灰度级范围为[0，L-1]数字图像直方图是离散函数h(r_k) = n_k，其中r_k是第k个灰度级(灰度值),n_k是图像中灰度级为r_k的像素个数,归一化的直方图为p(r_k) = n_k / (MN)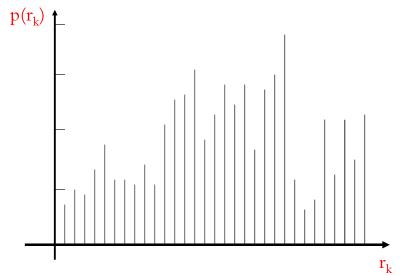


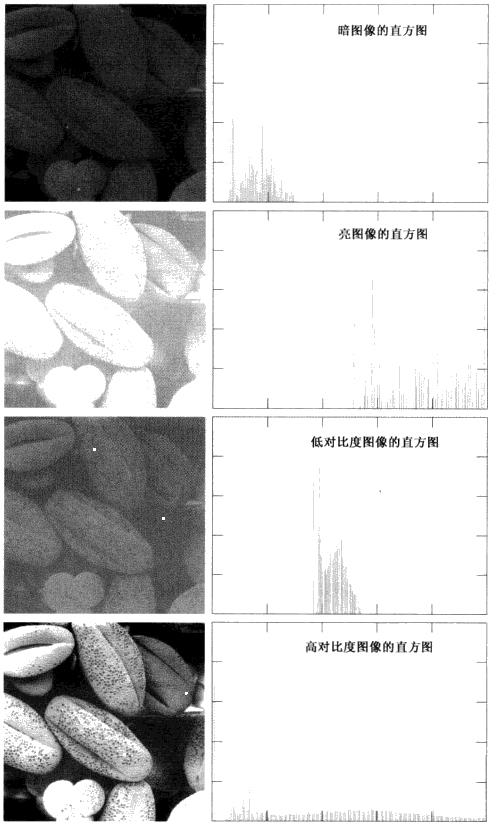
暗图像的直方图的分量集中在灰度级的低端,亮图像的直方图分量则倾向于灰度级的高端
高对比度图像直方图分量覆盖很宽的灰度级范围,且像素分布均匀,反之,低对比度图像直方图的分量覆盖较窄的灰度级范围,且像素分布不均匀
结论:若一幅图像倾向于占据整个可能的灰度级且分布均匀,则图像具有高对比度且灰色调具有较大变化

直方图均衡化

作用:使得图像的像素占有全部可能的灰度级且分布均匀,能够具有高对比度
方法:灰度级变换 s = T(r)
T(r)满足下列两个条件：
（1）T(r)在区间0 ≤ r ≤ L-1中为单值且单调递增
（2）当 0 ≤ r ≤ L-1时,0 ≤ T(r) ≤ L-1
条件(1)保证原图各灰度级在变换后仍保持从黑到白(或从白到黑)的排列次序
条件(2)保证变换前后灰度值动态范围的一致性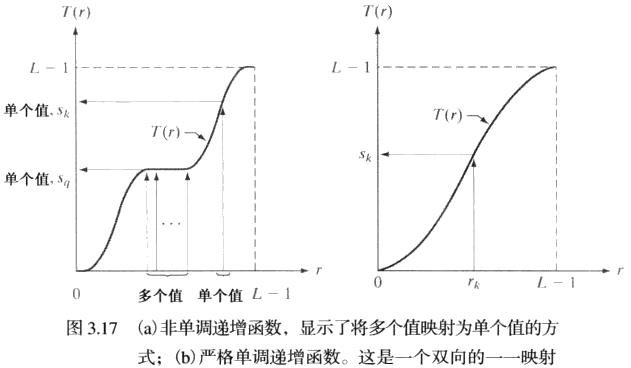

图像的灰度级可看成是区间[0,L-1]内的随机变量,随机变量的基本描绘是其概率密度函数
令p_r(r)为r的概率密度函数,p_s(s)是s的概率密度函数,p_r(r)和T(r)已知,在感兴趣的值域上T(r)是连续可微的,则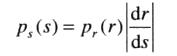

有如下变换函数T(r)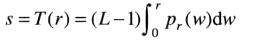

莱布尼茨准则可得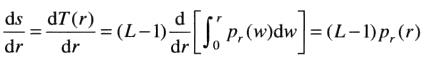


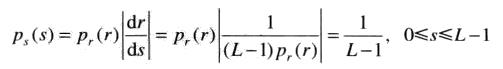
p_s(s)为均匀概率密度函数，即证明经上述灰度变换函数T(r),得到随机变量s由均匀概率密度函数表征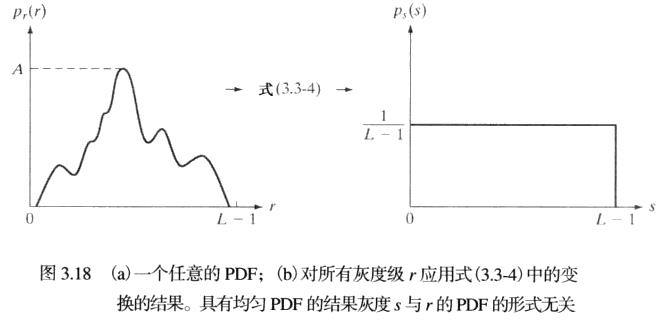

对于离散值,处理其概率(直方图值)与求和代替处理概率密度函数与积分
一幅数字图像中灰度级r_k出现的概率近视为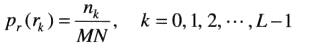

变换函数为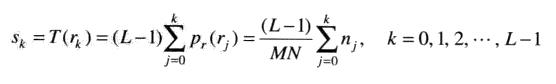

例子


均衡后的图像中有790个像素取s0=1值,同理有1023个像素取s1=3值,….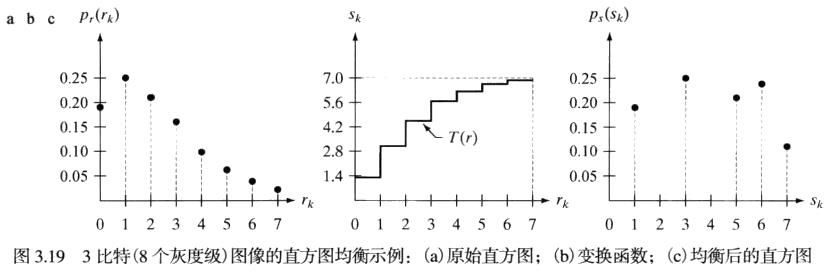

直方图规定化

直方图规定化是指经过处理后的图像具有规定的直方图形状
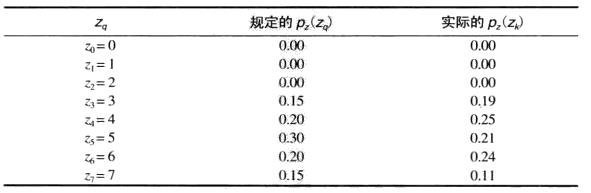
令p_r(r)为输入图像估计,p_z(z)为图像所具有的指定概率密度函数
有如下变换函数T(r)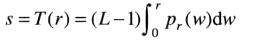

定义有如下特性的随机变量z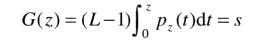

由G(z) = T(r)，z必须满足如下条件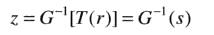

由一幅给定图像得到一幅其灰度级具有指定概率密度函数图像的步骤:
1.有输入图像得到p_r(r)，并由T(r)求得s值
2.由指定的PDF求得G(z)
3.求得G(z)的反函数z = G^{-1}(s)
4.利用T(r)对输入图像进行均衡得到输出图像,对均衡后的图像中具有s值的每个像素
执行反函数z = G^{-1}(s)
对于离散值: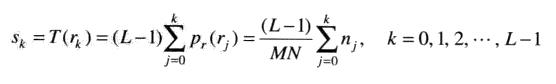


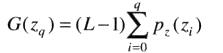
对一个q值: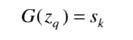

反函数为: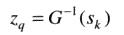

例子

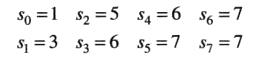
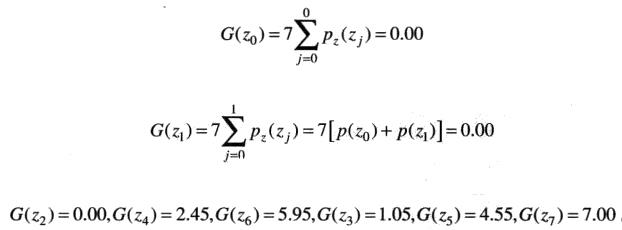
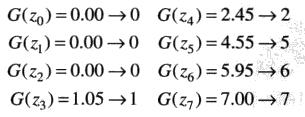
空间滤波

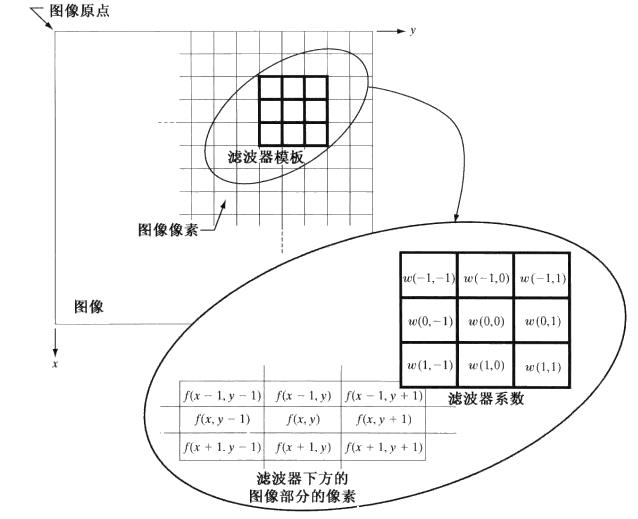
空间滤波器由一个邻域(较小的矩形)和对该邻域包围的图像像素执行预定义操作组成,滤波产生一个新像素,新像素的坐标等于邻域中心的坐标,像素值是滤波操作的结果.滤波器在图像上执行的是线性操作则称为线性空间滤波器,否则称为非线性空间滤波器.
例如,如下3 x 3领域的线性空间滤波器的处理机理，在图像中任意一点(x,y),滤波器的响应g(x,y)是滤波器系数与该滤波器包围的图像像素的乘积之和: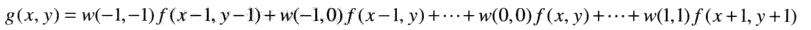

空间相关与卷积

相关是滤波器模板移过图像并计算每个位置乘积之和的处理,卷积的机理类似,但其滤波器首先要旋转180°
如下,显示了一个一维图像函数和一个一维滤波器,执行操作时,存在未覆盖的的部分函数,若滤波器的尺寸为m，则在需要在f的一侧补m-1个0

二维图像函数和二维滤波器

总结
大小为m x n的滤波器和一幅图像f(x,y)做相关操作,可表示为:
a = (m-1)/2,b = (n-1)/2 ，为表示方便,假设m和n是奇整数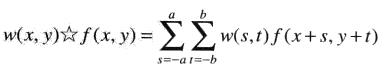

类似地，卷积表示为: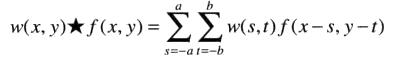

版权声明：原创,转载请注明来源,否则律师函警告

---