图像采样和量化

图像采样

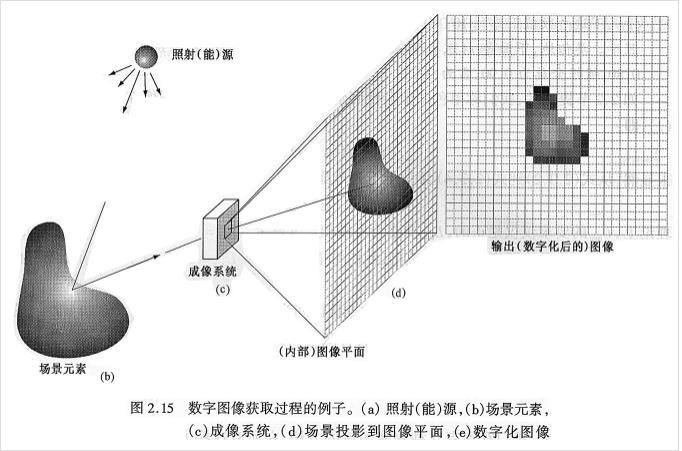
数字化坐标值称为采样,对二维空间中连续的图像在水平和垂直方向上等间距地分割成矩形网状结构，所形成的微小方格称为像素点,小方格中的值由灰度值(方格区域亮度的平均值)表示,采样的实质就是用多少个像素点来描述一幅图像.
采样时，若横向的像素数(列数)为M,纵向的像素数(行数)为N,则图像总像素数为M*N个像素；

采样间隔越大，即行列数少,则图像像素数越少，空间分辨率低，质量差，严重时出现马赛克效应；
采样间隔越小，即行列数大,则图像像素数越多，空间分辨率高，图像质量好，数据量大；
如下图,上述采样点分别为a:1024x1024 , b:512x512 , c:256x256 , d:128x128 , e:64x64, f:32x32

采样过程: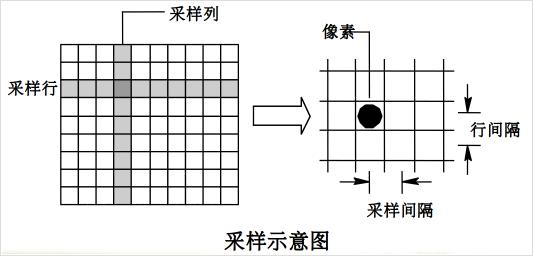

图像量化

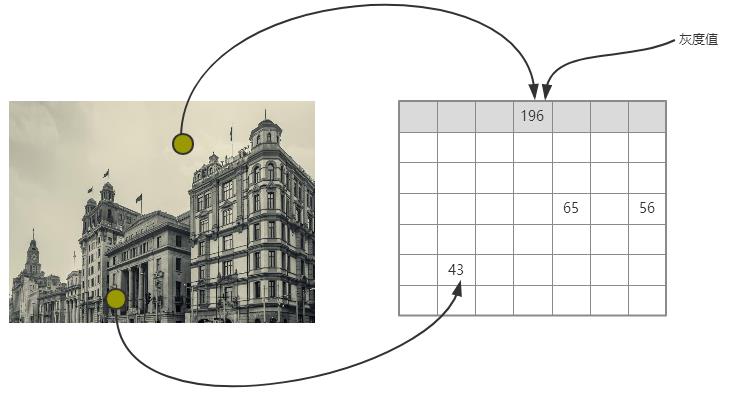
采样后所得各像素的灰度模拟量到离散量的转换为图像灰度量化
像素灰度级/灰度值/灰度:表示像素明暗程度的整数
灰度级数:数字图像中不同灰度值的个数(G）
若连续的灰度值用$z$表示,则满足于z{i} < z < z{i+1} 的z值都量化为整数值z{i}，z{i}称为像素灰度值
量化后的的灰度值用比特位数(g:存储图像灰度值所需的比特位数)表示,即$G=2^{g}$,如黑-灰-白的连续变化灰度值,用8位比特量化则为0~255个灰度值,代表相应的浓淡程度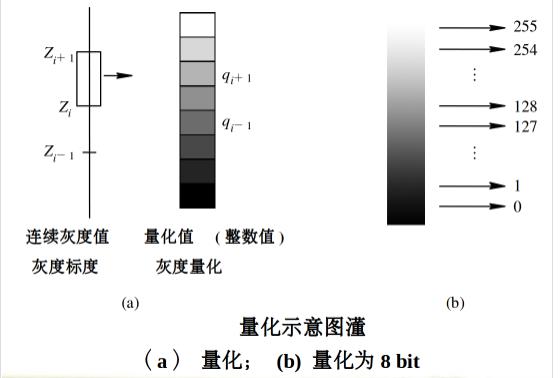

图像的数据量 = M x N x G bit

数字图像根据灰度级数的差异可分为黑白图像、灰度图像、彩色图像

• 黑白图像
  图像的每个灰度值/像素只能是黑或白,无中间值的过渡,故称二值图,灰度级数为2,灰度值为0或1
  
• 灰度图像
  图像的灰度级数大于2,但不包含彩色信息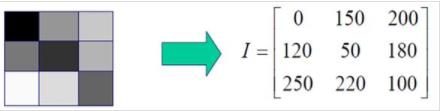
  
• 彩色图像
  每个灰度值由R、G、B分量构成,其中R、G、B由不同的灰度值来描述
  

量化等级越高,图像层次越丰富图像质量越好,反之图像质量差,如下图,量化等级依次递减所得的图像

---

数字图像表示

一幅M×N的图像可以表示为矩阵,矩阵中的每个元素为图像的灰度值(像素值)

空间和灰度分辨率

空间分辨率是图像中可辨别最小细节的度量,其中每单位距离线对数和每单位距离点数(像素数)是最通用的度量 —— 采样程度
灰度分辨率是指在灰度级中可分辨的最小变化 —— 量化程度

图像内插

图像内插是在诸如放大、收缩、旋转和几何校正等任务中广泛应用的工具
从根本上看,内插是用已知数据来估计未知位置数值的处理
源图像大小为M * N,目标图像为A * B,则两幅图像的边长比分别为:M/A和N/B,目标图像(i,j)像素可通过边长比对应回源图像,其对应坐标为(i * M / A,j * N / B)，显然,对应的坐标一般不是整数，而非整数的坐标无法在图像上使用.

最近邻内插法

假设一幅500x500的图像放大1.5倍到750x750，创建一个750x750的网格,其与原图有相同的间隔,然后将其收缩,使它准确地与原图匹配,显然收缩后的750x750网格的像素间隔小于原图的像素间隔,为了覆盖的每一个点赋以灰度值,因此在原图中寻找最接近的像素,并把该像素的灰度值赋给750x750网格中的新像素,完成像素的赋值后,再将图像扩展到规定的大小.
蓝色为原图网格,红色为放大后的网格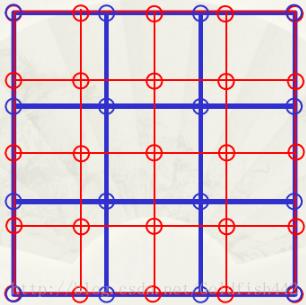

取最近的像素灰度值赋值给新像素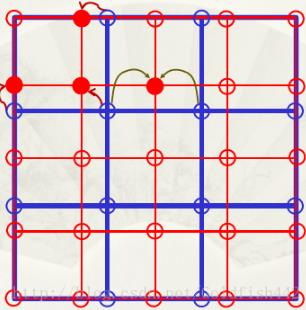

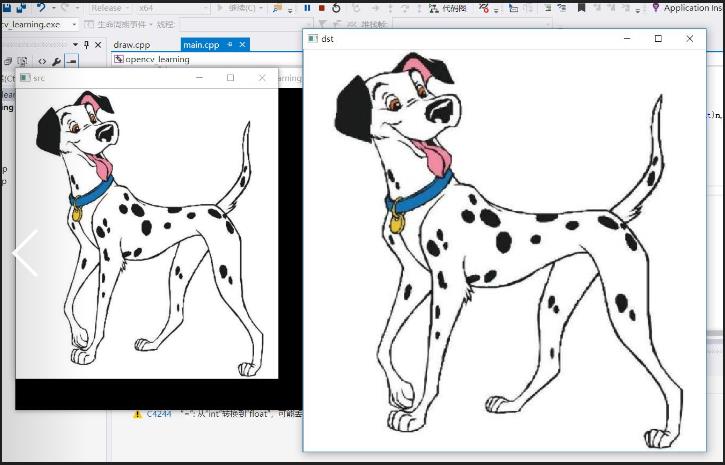
C++代码实现

#include<iostream>
#include<opencv2\opencv.hpp>
using namespace cv;
int main() {
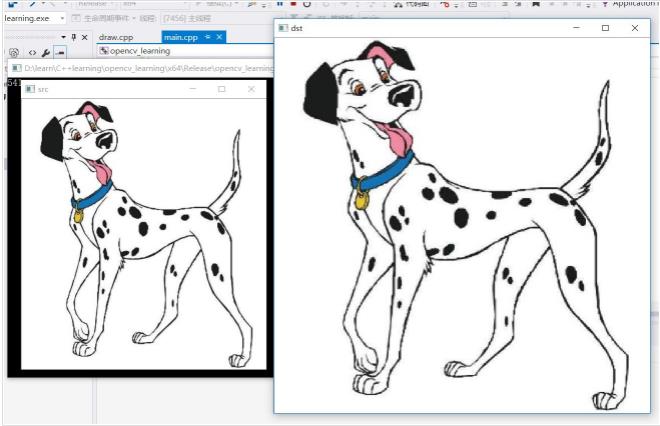
    Mat src = imread("D:/learn/jiaopan/source/images/opencv3/blob.jpg");//原图
    imshow("src", src);
    std::cout << src.rows;
    //创建网格矩阵
    Mat dst = Mat::zeros(Size(750, 750), CV_8UC3);
    //放大比例
    double fRows = 750 / (float)src.rows;
    double fCols = 750 / (float)src.cols;
    int primaryX = 0, primaryY = 0;

    //最近邻内插法
    for (int i = 0; i != dst.rows; i++) {
        for (int j = 0; j != dst.cols; j++){
            primaryX = cvRound(i / (double)fRows);
            primaryY = cvRound(j / (double)fCols);
            if (primaryX < src.rows && primaryX >= 0 && primaryY >= 0 && primaryY < src.cols){
                dst.at<cv::Vec3b>(i, j)[0] = src.at<cv::Vec3b>(primaryX, primaryY)[0];
                dst.at<cv::Vec3b>(i, j)[1] = src.at<cv::Vec3b>(primaryX, primaryY)[1];
                dst.at<cv::Vec3b>(i, j)[2] = src.at<cv::Vec3b>(primaryX, primaryY)[2];
            }
        }
    }
    imshow("dst", dst);

    waitKey(0);
    return 0;
}

双线性插值

双线性插值通过寻找距离对应坐标最近的四个像素点计算该点灰度值或者RGB值,如对应坐标是(2.5,4.5)，则最近的四个像素为 (2,4) , (2,5) , (3,4) , (3,5).
如图，已知Q11 (x1, y1), Q12 (x1, y2), Q21 (x2, y1), Q22 (x2, y2)，插值的点为P点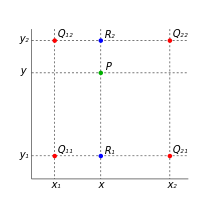

X方向

Y方向

先在 x 方向插值，再在 y 方向插值，其结果与按照上述顺序双线性插值的结果一致
若四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，插值公式可化简为

其矩阵运算公式为

双线性插值的结果不是线性的，它是两个线性函数的积，在单位正方形上，双线性插值可以记作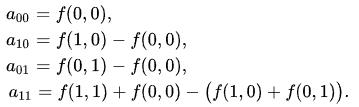


一般情况:

代码实现

#include<iostream>
#include<opencv2\opencv.hpp>
using namespace cv;
int main() {
    Mat src = imread("D:/learn/jiaopan/source/images/opencv3/blob.jpg");//原图
    imshow("src", src);

    //创建网格矩阵
    Mat dst = Mat::zeros(Size(750, 750), CV_8UC3);


    //放大比例
    double fRows = 750 / (float)src.rows;
    double fCols = 750 / (float)src.cols;
    int primaryX = 0, primaryY = 0;

    //双线性插值
    float m = 0;
    float n = 0;
    CvScalar a, b, c, d;
    for (int i = 0; i != dst.rows; i++) {
        for (int j = 0; j != dst.rows; j++) {
            m = cvRound(i / (double)fRows);
            n = cvRound(j / (double)fCols);
            double ux = m - (int)m;
            double uy = n - (int)n;

            if (m >= 0 && m <= src.rows - 1 && n >= 0 && n <= src.cols - 1) {
                a = src.at<cv::Vec3b>((int)m, (int)n);
                b = src.at<cv::Vec3b>((int)m, (int)n + 1) - src.at<cv::Vec3b>((int)m, (int)n);
                c = src.at<cv::Vec3b>((int)m + 1, (int)n) - src.at<cv::Vec3b>((int)m, (int)n);
                d = src.at<cv::Vec3b>((int)m + 1, (int)n + 1) - src.at<cv::Vec3b>((int)m + 1, (int)n) - src.at<cv::Vec3b>((int)m, (int)n + 1) + src.at<cv::Vec3b>((int)m, (int)n);

                b.val[0] = b.val[0] * uy;
                b.val[1] = b.val[1] * uy;
                b.val[2] = b.val[2] * uy;
                c.val[0] = c.val[0] * ux;
                c.val[1] = c.val[1] * ux;
                c.val[2] = c.val[2] * ux;
                d.val[0] = d.val[0] * ux*uy;
                d.val[1] = d.val[1] * ux*uy;
                d.val[2] = d.val[2] * ux*uy;
            }
            dst.at<cv::Vec3b>(i, j)[0] = (int)(a.val[0] + b.val[0] + c.val[0] + d.val[0]);
            dst.at<cv::Vec3b>(i, j)[1] = (int)(a.val[1] + b.val[1] + c.val[1] + d.val[1]);
            dst.at<cv::Vec3b>(i, j)[2] = (int)(a.val[2] + b.val[2] + c.val[2] + d.val[2]);
        }
    }
    imshow("dst", dst);
    waitKey(0);
    return 0;
}

双三次内插

双三次内插包括16个最近邻点,在保持细节方面比双线性内插更好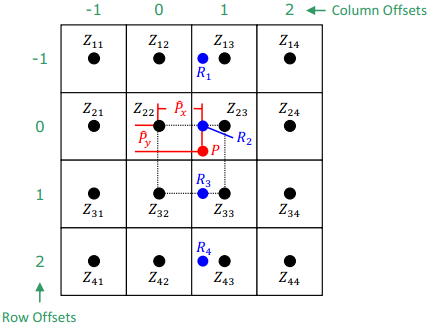

https://en.wikipedia.org/wiki/Bicubic_interpolation

像素间的基本关系

相邻像素

位于坐标(x,y)处的像素p有4个水平和垂直的相邻像素(4邻域 N4(p)),其坐标公式如下

(x+1,y),(x-1,y),(x,y+1),(x,y-1)

p的4个对角相邻像素(对角邻域)的坐标公式如下:

(x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1)

邻接性

令V是用于定义邻接性的灰度值集合,在二值图像中,把具有1值的像素归为邻接像素,则V = {1}

4邻接:若q在集合N4(p)中，则具有V中数值(1)的两个像素p和q是4邻接
8邻接:若q在集合N8(p)中，则具有V中数值(1)的两个像素p和q是8邻接(8邻域=4邻域+对角邻域）
m邻接:若q在N4(p)中，或者在ND(p)中，且集合N4(p) ∩ N4(q) 没有V中数值(1)的像素，则具有V中数值的两个像素p和q是m邻接的

距离度量

对于像素p、q和z，分别具有坐标(x,y)，(s,t)和(u,v)，若
(1) D(p,q) ≥ 0 (D(p,q)=0，当且仅当p =q)
(2) D(p,q) = D(q,p)
(3) D(p,z) ≤ D(p,q) + D(q,z)
则称D是距离函数或度量

欧式距离

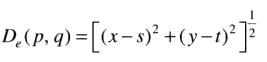
距离点(x,y)的距离小于或等于某个值r的像素点是在圆心为(x,y)且半径为r的圆平面内

城市距离

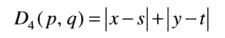
距离点(x,y)的距离小于或等于某个值r的像素点形成一个中心为(x,y)的菱形
如图,与点(x,y)的距离小于或等于2的像素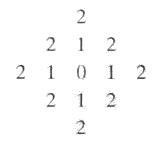

棋盘距离

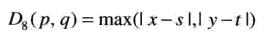
距离点(x,y)的距离小于或等于某个值r的像素点形成一个中心为(x,y)的方形
如图,与点(x,y)的距离小于或等于2的像素

版权声明：原创,转载请注明来源,否则律师函警告

---